Mathematical and Algorithmic Methodologies for Computing Multiphase Multiphysics
Industrial Foams, Materials, Manufacturing, and Cell Mechanics

An example computation for fluid flow and interface forces in agitators for fluid mixing in industrial devices.
Many problems involve the physics of multiply-connected moving interfaces. Examples include liquid foams (e.g. soap bubbles, polyurethane and colloidal mixtures), and solid foams, such as wood and bone. Manufactured solid foams lead to lightweight cellular engineering materials, including crash absorbent aluminum foams, and controlling foams is critical in chemical processing.
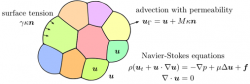
Diagram showing the components of the Navier-Stokes equation, which includes velocity u, and surface tension. (Select to enlarge.)
These problems have multiple domains which share common walls meeting in multiple junctions. Boundaries move under forces which depend on both local and global geometric properties, such as surface tension and volume constraints, as well long-range physical forces, including incompressible flow, membrane permeability, and elastic forces. As an example, the interaction of multiple phases in fluid simulations requires a robust treatment of the interplay between membrane dynamics, fluid mechanics, surface tension, and intricate jump conditions.
Producing good mathematical models and numerical algorithms that capture the motion of these interfaces is challenging, especially at junctions where multiple interfaces meet, and when topological connections change. Methods have been proposed, including front tracking, volume of fluid, variational, and level set methods. It has remained a challenge to robustly and accurately handle the wide range of possible motions of an evolving, highly complex, multiply-connected interface separating a large number of phases under time-resolved physics.
CRD Math researchers have recently built a computational methodology, known as the Voronoi Implicit Interface Method, to track multiple coupled interfaces moving under complex physics constraints. Mathematically, they provide a consistent formulation of 3D multiphase physics as a single time-dependent PDE, which is solved using intertwined steps of initial value upwind solvers and fast Eikonal solvers for Voronoi reconstructions. The results are algorithms which efficiently and accurately compute topological change while coupling to fluid and solid mechanics, surface tension, and geometrical constraints. The methods are highly efficient and parallelizable. The methods are now being used to compute industrial mixing and materials manufacturing. The original paper was awarded the 2011 Proceedings of the National Academy Sciences Cozzarelli Prize for Best Paper in Applied Sciences and Engineering.

3D incompressible fluid mixing of various density phases under gravity and surface tension.
Such algorithms allow for a more accurate understanding of a vast array of science problems and applications. The algorithms are applicable to many computing problems in both industry and research, including fluid mixing of multiple species in combustion and reactor designs, grain metal and materials growth in industrial manufacturing, semiconductor failure analysis of metal interconnect lines, liquid foam drainage in chemical and biological devices, and cell mechanics and structural stability analyses in biofuels.
About Berkeley Lab
Founded in 1931 on the belief that the biggest scientific challenges are best addressed by teams, Lawrence Berkeley National Laboratory and its scientists have been recognized with 16 Nobel Prizes. Today, Berkeley Lab researchers develop sustainable energy and environmental solutions, create useful new materials, advance the frontiers of computing, and probe the mysteries of life, matter, and the universe. Scientists from around the world rely on the Lab’s facilities for their own discovery science. Berkeley Lab is a multiprogram national laboratory, managed by the University of California for the U.S. Department of Energy’s Office of Science.
DOE’s Office of Science is the single largest supporter of basic research in the physical sciences in the United States, and is working to address some of the most pressing challenges of our time. For more information, please visit energy.gov/science.









