Share
symPACK Sparse Symmetric Direct Solver
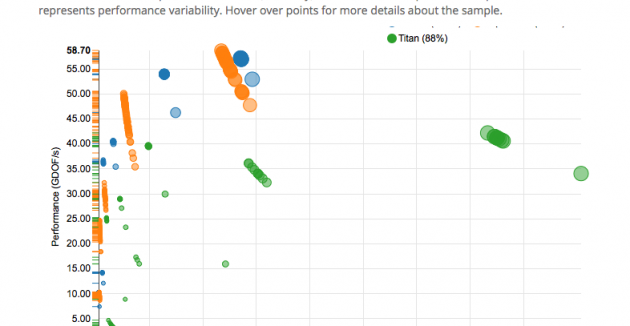
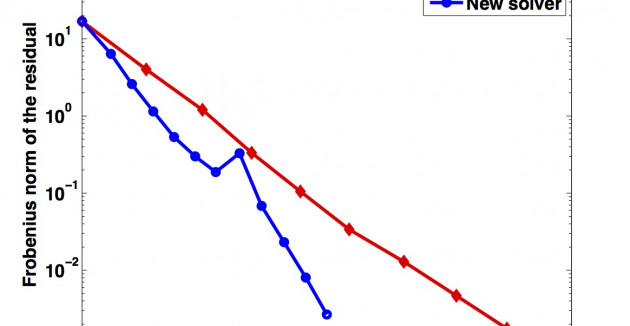
We developed and a new direct linear solver for sparse symmetric positive definite matrices, symPACK. By exploiting the symmetry explicitly, symPACK achieves low storage costs.
SuperLU Sparse Unsymmetric Direct Solver
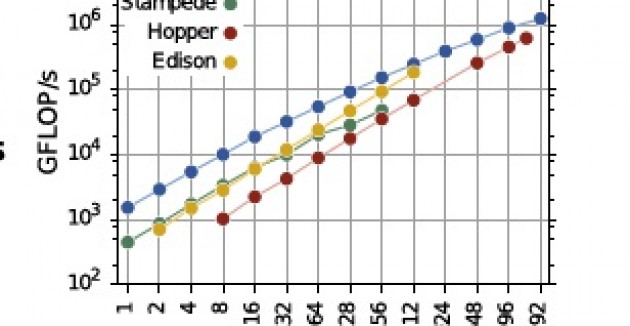
The recently developed communication-avoiding 3D sparse LU factorization in SuperLU_DIST reduces latency, achieving speedups up to 27x for planar graphs and up to 2.5x for non-planar graphs over the b…
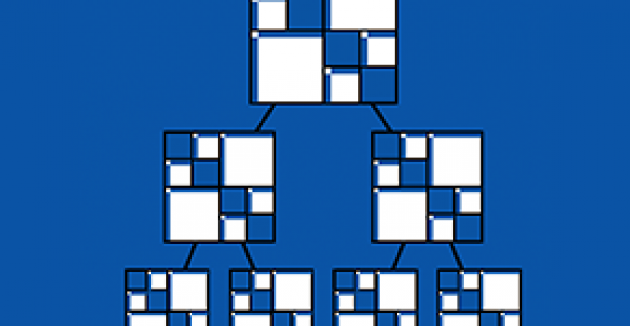
Sparse Low-rank Hierarchical Matrix Preconditioner
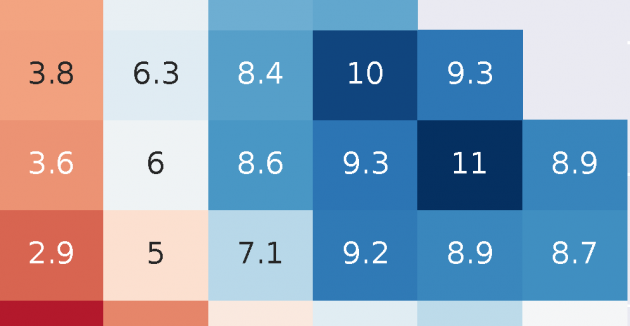
STRUMPACK (STRUctured Matrices PACKage) software uses faster algorithms developed in SSG using hierarchical low-rank matrix algebra, which generalizes fast multipole methods and leads to factorization…
Solvers for Edge Plasma Simulation
Researchers in the Scalable Solvers Group at LBNL help the SciDAC application partnership Center for Edge Plasma Simulation (EPSI) by developing solvers for advanced fusion simulation codes based upon…
High Performance Geometric Multigrid
Research scientists at LBNL and Argonne National Laboratory have developed a new high performance computing metric intended to provide the community with both a ranking metric for the world's largest …
Accelerating Eigenpair Computations
Novel approach developed by SciDAC FASTMath Institute accelerates computations of large numbers of extreme eigenpairs of Hermitian operators. The new eigenvalue solver has been tested in the framework…
HipGISAXS
The recently developed HipGISAXS software is an unique massively parallel code to simulate and analyze custom and complex morphologies from Grazing Incidence Small Angle X-ray Scattering (GISAXS) expe…
Our Mission
Develop efficient linear and eigensolver algorithms and fast, scalable, library implementations. Integrate the new algorithms and software into DOE applications.
Current expertise in SSG includes:
- Dense linear algebra
- Factorization-based sparse solvers and preconditions
- Multigrid methods
- Sparse eigensolvers
- Optimization, machine learning
- Communication-avoiding algorithms (see, e.g., http://bebop.cs.berkeley.edu/)
- Mathematical software
Group Leader: X. Sherry Li
Position openings
None right now.
