Solving Poisson's Equation using Adaptive Mesh Refinement (AMR)

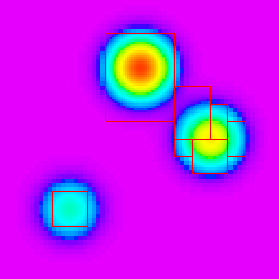
Many physical problems have variations in scale. When solving these problems numerically, high grid resolution is needed to adequately solve the equations. However, there are often also large portions of the domain where high levels of refinement are not needed; using a highly refined mesh in these regions represents a waste of computational effort. Limitations on computational resources often force a compromise on grid resolution, resulting in under-resolution of the problem. By locally refining the mesh only where needed, Adaptive Mesh Refinement (AMR) allows concentration of effort where it is needed, allowing better resolution of the problem.

Solutions to Poisson's equation, for example, can exhibit this type of variation, due to local concentration of charges or boundary conditions. Unfortunately, local refinement introduces several added issues like matching of the solution at grid interfaces.

For an exploration of the issues involved in solving elliptic problems using AMR, as well as a detailed explanation of our algorithm for solving Poisson's equation using AMR (based on the block-structured AMR strategies of Berger & Colella), click here for a postscript document (last updated 10/24/96). Or, click here for the HTML version (Thanks to Rick Propp for doing the latex2html conversion...)

We have developed an AMR Poisson solver code which solves Poisson's equation using multigrid relaxation. To decide where grid refinement should be added, there are three options. First, the user can predefine a grid hierarchy. If adaptive grid generation is desired, the code can locate places where the error in a coarse solution is high based on either Richardson extrapolation or on a user supplied criterion.

For a zipped tarfile of the AMR Poisson solver code, click here . For the a gzipped version of the same thing, click here . For html documentation of this code, click here. For a postscript "manual" of the code, click here. This code uses the Boxlib library of C++ classes developed for managing data on rectangular domains by the Center for Computational Science and Engineering at the National Energy Research Supercomputer Center .
(code last modified 5/29/97)

If you do grab the code, I suggest you e-mail me and let me know so I can put you on my mailing list for bug-fixes and changes (the code appears to be fairly stable, but ya never know...).

.. NOTE (6/09/03): I haven't tried compiling the AMRPoisson code with the latest BoxLib distribution, so I don't know whether it still works. There is a new version of the AMRPoisson code which uses the same algorithm included in the Chombo software package, which I recommend for those looking for AMR development tools. For more details, or for the current status of things, e-mail me, and I'll fill you in...

NOTE (1/19/10): At this point, the code in the tarfile on this page is more than 10 years old and is guaranteed not to compile with any currently available Boxlib or Chombo distribution. I've left it up in case anyone is interested for historical reasons. Please don't ask current CCSE members for the incredibly out-dated version of BoxLib which would be required to actually compile this code. If you'd like a currently available, fully-supported, parallel (and scalable!) AMR elliptic solver which follows the algorithm implemented here, try the Chombo software package, which is is a full-featured AMR software development package.

Also, there is a separate website devoted to my thesis, "An Adaptive Cell-centered Projection Method for the Incompressible Euler Equations", which also explores the issues involved in adaptive solutions to Poisson's equation in more depth.

For any questions, comments, or further information, email me at dfmartin@lbl.gov

References:

A. Almgren, T. Buttke, and P. Colella. A fast adaptive vortex method in three dimensions. Journal of Computational Physics, 113:177-200, 1994.

J. Bell, M. J. Berger, J. Saltzman, and M. Welcome, Three dimensional adaptive mesh refinement for hyperbolic conservation laws. J. Sci. Comput., 15(1):127-138, January, 1994.

M. J. Berger and I. Rigoutsos, An algorithm for point clustering and grid generation, IEEE Transactions Systems, Man and Cybernetics, 21(5):1278-1286, 1991.

M.J. Berger and P. Colella. Local adaptive mesh refinement for shock hydrodynamics. J. Comput. Phys., 82(1):64-84.

M.J. Berger and J. Oliger. Adaptive mesh refinement for hyperbolic partial differential equations. J. of Comput. Phys., 53, 1984.

W.L. Briggs, A Multigrid Tutorial. SIAM, Philadelphia, 1987.

C. Rendleman, V. Beckner, J. Bell, B. Crutchfield, L. Howell, and M. Welcome. Boxlib Users Guide and Manual: A Library for Managing Rectangular Domains. edition 1.99, for boxlib version 1.99, Center for Computational Science and Engineering, Lawrence Livermore National Laboratory 1995. http://SEESAR.LBL.GOV/ccse/software/software.html .

Acknowledgements:

This work has been supported by the Computational Science Graduate Fellowship Program of the Department of Energy and the following grants:

"Adaptive Numerical Methods for Partial Differential Equations," US Department of Energy Mathematical, Computing, and Information Sciences Division, Grant DE-FG03-94ER25205.

"Computational Fluid Dynamics and Combustion Dynamics," US Department of Energy High-Performance Computing and Communications Grand Challenge Program, Grant DE-FG03-92ER25140.